what do you think would happen to the mass of the reaction took place inside a sealed plastic bag
Gas Laws
Boyle's Law
Torricelli's experiment did more than only show that air has weight; it also provided a way of creating a vacuum because the infinite higher up the column of mercury at the meridian of a barometer is well-nigh completely empty. (It is free of air or other gases except a negligible amount of mercury vapor.) Torricelli'due south work with a vacuum soon caught the eye of the British scientist Robert Boyle.
Boyle'due south almost famous experiments with gases dealt with what he called the "leap of air." These experiments were based on the observation that gases are rubberband. (They return to their original size and shape after being stretched or squeezed.) Boyle studied the elasticity of gases in a J-tube like to the apparatus shown in the effigy below. By adding mercury to the open up stop of the tube, he trapped a minor volume of air in the sealed end.

Boyle studied what happened to the book of the gas in the sealed cease of the tube equally he added mercury to the open stop.
Boyle noticed that the product of the force per unit area times the volume for any measurement in this table was equal to the production of the pressure level times the volume for any other measurement, within experimental error.
P ane V 1 = P 2 Five 2
This expression, or its equivalent,
![]()
is now known as Boyle's Constabulary.
![]()
Amonton's Law
Toward the end of the 1600s, the French physicist Guillaume Amontons built a thermometer based on the fact that the pressure of a gas is directly proportional to its temperature. The human relationship between the pressure level and the temperature of a gas is therefore known every bit Amontons' police force.
P ![]() T
T
Amontons' law explains why machine manufacturers recommend adjusting the pressure of your tires before you offset on a trip. The flexing of the tire equally you lot drive inevitably raises the temperature of the air in the tire. When this happens, the pressure of the gas inside the tires increases.
Amontons' law can be demonstrated with the apparatus shown in the figure below, which consists of a pressure gauge connected to a metal sphere of constant volume, which is immersed in solutions that accept different temperatures.
 |
| The apparatus for demonstrating Amonton'due south constabulary consists of . |
The following information were obtained with this apparatus.
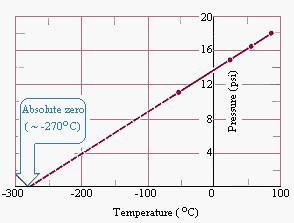
In 1779 Joseph Lambert proposed a definition for absolute zero on the temperature scale that was based on the direct-line relationship between the temperature and pressure of a gas shown in the figure above.
He defined absolute zero as the temperature at which the pressure of a gas becomes cipher when a plot of force per unit area versus temperature for a gas is extrapolated. The pressure level of a gas approaches cypher when the temperature is well-nigh -270C. When more accurate measurements are fabricated, the pressure of a gas extrapolates to zero when the temperature is -273.15C. Absolute cipher on the Celsius scale is therefore -273.15C.
The relationship between temperature and pressure can be profoundly simplified by converting the temperatures from the Celsius to the Kelvin scale.
T K = T o C + 273.15
When this is done, a plot of the temperature versus the pressure of a gas gives a straight line that passes through the origin. Any two points along the line therefore fit the post-obit equation.
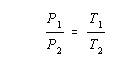
It is important to remember that this equation is only valid if the temperatures are converted from the Celsius to the Kelvin scale before calculations are washed.
![]()
Charles' Law
On 5 June 1783, Joseph and Etienne Montgolfier used a burn down to inflate a spherical balloon well-nigh 30 anxiety in bore that traveled nearly a mile and one-half earlier it came back to world. News of this remarkable accomplishment spread throughout France, and Jacques-Alexandre-Cesar Charles immediately tried to duplicate this operation. As a result of his work with balloons, Charles noticed that the volume of a gas is directly proportional to its temperature.
Five ![]() T
T
This relationship between the temperature and volume of a gas, which became known as Charles' law, provides an explanation of how hot-air balloons work. Ever since the 3rd century B.C., information technology has been known that an object floats when it weighs less than the fluid it displaces. If a gas expands when heated, then a given weight of hot air occupies a larger volume than the same weight of cold air. Hot air is therefore less dense than cold air. Once the air in a balloon gets hot plenty, the net weight of the airship plus this hot air is less than the weight of an equivalent volume of cold air, and the balloon starts to ascension. When the gas in the balloon is immune to cool, the airship returns to the ground.
Charles' law can be demonstrated with the apparatus shown in the figure below. A thirty-mL syringe and a thermometer are inserted through a rubber stopper into a flask that has been cooled to 0C. The water ice bath is so removed and the flask is immersed in a warm-water bathroom. The gas in the flask expands equally information technology warms, slowly pushing the piston out of the syringe. The total book of the gas in the system is equal to the volume of the flask plus the volume of the syringe.
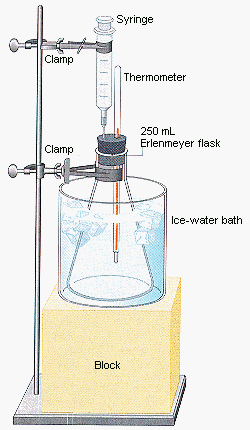
The figure below shows a plot of the typical data obtained from this experiment.

This graph provides u.s.a. with another fashion of defining absolute zero on the temperature calibration. Absolute nil is the temperature at which the volume of a gas becomes naught when the a plot of the volume versus temperature for a gas are extrapolated. As expected, the value of absolute null obtained past extrapolating the information is essentially the same as the value obtained from the graph of pressure versus temperature in the preceding section. Absolute goose egg can therefore exist more accurately defined as the temperature at which the pressure and the volume of a gas extrapolate to nix.
A plot of the volume versus the temperature of a gas (when the temperatures obtained are converted from Celsius to the Kelvin scale) becomes a straight line that passes through the origin. Whatever two points along this line tin therefore exist used to construct the following equation, which is known every bit Charles' law.

Earlier using this equation, it is important to remember that temperatures must be converted from C to M.
![]()
Gay-Lussac's Police force
Joseph Louis Gay-Lussac (1778-1850) began his career in 1801 by very advisedly showing the validity of Charles' law for a number of different gases. Gay-Lussac'southward most of import contributions to the report of gases, however, were experiments he performed on the ratio of the volumes of gases involved in a chemical reaction.
Gay-Lussac studied the volume of gases consumed or produced in a chemical reaction because he was interested in the reaction betwixt hydrogen and oxygen to form water. He argued that measurements of the weights of hydrogen and oxygen consumed in this reaction could be influenced by the moisture present in the reaction flask, merely this moisture would non affect the volumes of hydrogen and oxygen gases consumed in the reaction.
Much to his surprise, Gay-Lussac establish that 199.89 parts by volume of hydrogen were consumed for every 100 parts by volume of oxygen. Thus, hydrogen and oxygen seemed to combine in a simple 2:one ratio by volume.
| hydrogen | + | oxygen | | water |
| two volumes | ane volume |
Gay-Lussac found similar whole-number ratios for the reaction between other pairs of gases. The chemical compound we now know as hydrogen chloride (HCl) combined with ammonia (NH3) in a uncomplicated ane:1 ratio by volume:
| hydrogen chloride | + | ammonia | | ammonium chloride |
| 1 volume | 1 volume |
Carbon monoxide combined with oxygen in a 2:i ratio by volume:
| carbon monoxide | + | oxygen | | carbon dioxide |
| ii volumes | i volume |
Gay-Lussac obtained like results when he analyzed the volumes of gases given off when compounds decomposed. Ammonia, for example, decomposed to give three times every bit much hydrogen by volume as nitrogen:
| ammonia | | nitrogen | + | hydrogen |
| i volume | 3 volumes |
On 31 December 1808, Gay-Lussac announced his police force of combining volumes to a meeting of the Societ Philomatique in Paris. At that time, he summarized the law equally follows: Gases combine among themselves in very simple proportions. Today, Gay-Lussac's law is stated as follows: The ratio of the volumes of gases consumed or produced in a chemic reaction is equal to the ratio of simple whole numbers.
![]()
Avogadro's Hypothesis
Gay-Lussac's law of combining volumes was announced but a few years after John Dalton proposed his atomic theory. The link betwixt these two ideas was first recognized by the Italian physicist Amadeo Avogadro three years later, in 1811. Avogadro argued that Gay-Lussac'southward police force of combining volumes could be explained past assuming that equal volumes of different gases collected under similar conditions comprise the aforementioned number of particles.
HCl and NH3 therefore combine in a 1:one ratio past volume because 1 molecule of HCl is consumed for every molecule of NH3 in this reaction and equal volumes of these gases contain the same number of molecules.
| NHiii(g) | + | HCl(g) | | NHfourCl(southward) |
Anyone who has blown up a balloon should accept the notion that the volume of a gas is proportional to the number of particles in the gas.
5 ![]() n
n
The more air you add to a balloon, the bigger it gets. Unfortunately this case does not test Avogadro'southward hypothesis that equal volumes of different gases contain the aforementioned number of particles. The best way to probe the validity of this hypothesis is to measure the number of molecules in a given volume of different gases, which can exist done with the appliance shown in the effigy beneath.

A small hole is drilled through the plunger of a 50-mL plastic syringe. The plunger is then pushed into the syringe and the syringe is sealed with a syringe cap. The plunger is and then pulled out of the syringe until the volume reads fifty mL and a nail is inserted through the hole in the plunger so that the plunger is not sucked dorsum into the barrel of the syringe. The "empty" syringe is then weighed, the syringe is filled with 50 mL of a gas, and the syringe is reweighed. The departure betwixt these measurements is the mass of 50 mL of the gas.
The results of experiments with six gases are given in the tabular array below.
Experimental Data for the Mass of fifty-mL Samples of Different Gases
| Compound | Mass of 50 mL of Gas (grand) | Molecular Weight of Gas | Number of Gas Molecules | |||
| Htwo | 0.005 | 2.02 | 1 ten 1021 | |||
| Northtwo | 0.055 | 28.01 | 1.2 x 1021 | |||
| O2 | 0.061 | 32.00 | one.1 x x21 | |||
| CO2 | 0.088 | 44.01 | 1.2 ten x21 | |||
| C4Hten | 0.111 | 58.12 | 1.15 10 1021 | |||
| CCl2F2 | 0.228 | 120.91 | 1.14 10 ten21 |
The number of molecules in a fifty-mL sample of whatsoever one of these gases can be calculated from the mass of the sample, the molecular weight of the gas, and the number of molecules in a mole. Consider the following calculation of the number of H2 molecules in 50 mL of hydrogen gas, for example.

The last column in the table to a higher place summarizes the results obtained when this calculation is repeated for each gas. The number of significant figures in the respond changes from one calculation to the adjacent. Only the number of molecules in each sample is the same, within experimental error. We therefore conclude that equal volumes of different gases collected under the same conditions of temperature and pressure level do in fact contain the aforementioned number of particles.
![]()
The Platonic Gas Equation
Gases can described in terms of four variables: pressure (P), book (V), temperature (T), and the amount of gas (due north). There are five relationships between pairs of these variables in which two of the variables were allowed to cahnge while the other 2 were held constant.
Each of these relationships is a special case of a more general relationship known as the ideal gas equation.
PV = nRT
In this equation, R is a proportionality constant known as the ideal gas constant and T is the absolute temperature. The value of R depends on the units used to express the four variables P, V, n, and T. By convention, most chemists use the following fix of units.
| P: atmospheres |
| T: kelvin |
| V: liters |
| n: moles |
![]()
Platonic Gas Calculations
The platonic gas equation can be used to predict the value of any one of the variables that describe a gas from known values of the other three.
The key to solving platonic gas problems ofttimes involves recognizing what is known and deciding how to utilize this information.
The ideal gas equation can be applied to bug that don't seem to ask for one of the variables in this equation.
The ideal gas equation can even exist used to solve bug that don't seem to contain plenty information.
Gas police problems oftentimes ask y'all to predict what happens when 1 or more changes are made in the variables that depict the gas. There are two ways of working these issues. A powerful approach is based on the fact that the ideal gas constant is in fact a constant.
We kickoff by solving the ideal gas equation for the ideal gas abiding.
![]()
We then note that the ratio of PV/nT at any fourth dimension must be equal to this ratio at any other fourth dimension.

Nosotros then substitute the known values of pressure, temperature, volume, and amount of gas into this equation and solve for the appropriate unknown. This approach has two advantages. First, simply ane equation has to be remembered. 2d, information technology tin can be used to handle bug in which more than than one variable changes at a time.
![]()
Dalton's Constabulary of Partial Pressures
The CRC Handbook of Chemistry and Physics describes the atmosphere every bit 78.084% Nii, twenty.946% Oii, 0.934% Ar, and 0.033% CO2 by book when the water vapor has been removed. What image does this description evoke in your heed? Do y'all believe that only 20.463% of the room in which y'all are sitting contains O2? Or do you believe that the atmosphere in your room is a more or less homogeneous mixture of these gases?
Gases expand to fill up their containers. The volume of O2 in your room is therefore the same equally the volume of N2. (Both gases aggrandize to make full the room.) When nosotros describe the atmosphere as 20.946% Oii past book, we mean that the volume of the atmosphere would compress by xx.946% if the O2 is removed.
What about the pressure of the different gases in your room? Is the pressure level of the O2 in the atmosphere the same as the pressure of the Ntwo? We can answer this question past rearranging the ideal gas equation every bit follows.
![]()
According to this equation, the pressure of a gas is proportional to the number of moles of gas, if the temperature and volume are held constant. Considering the temperature and volume of the Otwo and N2 in the atmosphere are the same, the pressure of each gas must be proportional to the number of the moles of the gas. Because there is more N2 in the atmosphere than Oii, the contribution to the total pressure of the atmosphere from Northtwo is larger than the contribution from O2.
John Dalton was the outset to recognize that the full pressure of a mixture of gases is the sum of the contributions of the individual components of the mixture. By convention, the office of the total pressure of a mixture that results from ane component is chosen the fractional pressure of that component. Dalton's constabulary of partial pressures states that the full pressure of a mixture of gases is the sum of the partial pressures of the various components.
P T = P 1 + P ii + P 3 + ...
Dalton derived the law of partial pressures from his work on the amount of water vapor that could exist absorbed by air at different temperatures. It is therefore plumbing equipment that this law is used near often to correct for the amount of water vapor picked up when a gas is collected past displacing h2o. Suppose, for example, that we want to collect a sample of O2 prepared past heating potassium chlorate until information technology decomposes.
| 2 KClO3(south) | | 2 KCl(southward) | + | iii O2(yard) |
The gas given off in this reaction can be collected by filling a flask with water, inverting the flask in a trough, and then letting the gas bubble into the flask as shown in the figure below.

Because some of the water in the flask volition evaporate during the experiment, the gas that collects in this flask is going to exist a mixture of O2 and h2o vapor. The total pressure of this gas is the sum of the partial pressures of these two components.
P T = P oxygen + P water
The total pressure level of this mixture must be equal to atmospheric pressure. (If information technology was any greater, the gas would push water out of the container. If information technology was any less, water would be forced into the container.) If we had some way to estimate the partial pressure of the water in this system, we could therefore calculate the partial pressure level of the oxygen gas.
By convention, the partial pressure of the gas that collects in a closed container to a higher place a liquid is known every bit the vapor pressure of the liquid. If we know the temperature at which a gas is collected by displacing water, and we presume that the gas is saturated with water vapor at this temperature, we can calculate the partial pressure of the gas by subtracting the vapor pressure of water from the full pressure of the mixture of gases collected in the experiment.
![]()
Source: https://chemed.chem.purdue.edu/genchem/topicreview/bp/ch4/gaslaws.php
Post a Comment for "what do you think would happen to the mass of the reaction took place inside a sealed plastic bag"